Eng Lang Setup Ex Rmd 計算機言語の実行記録の収集
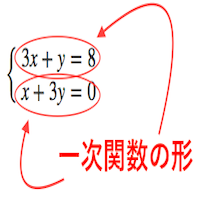
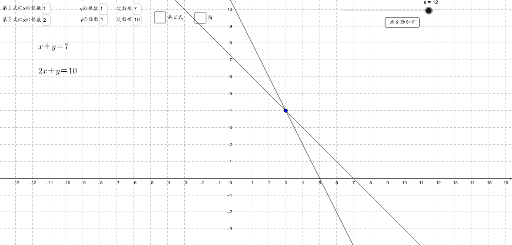
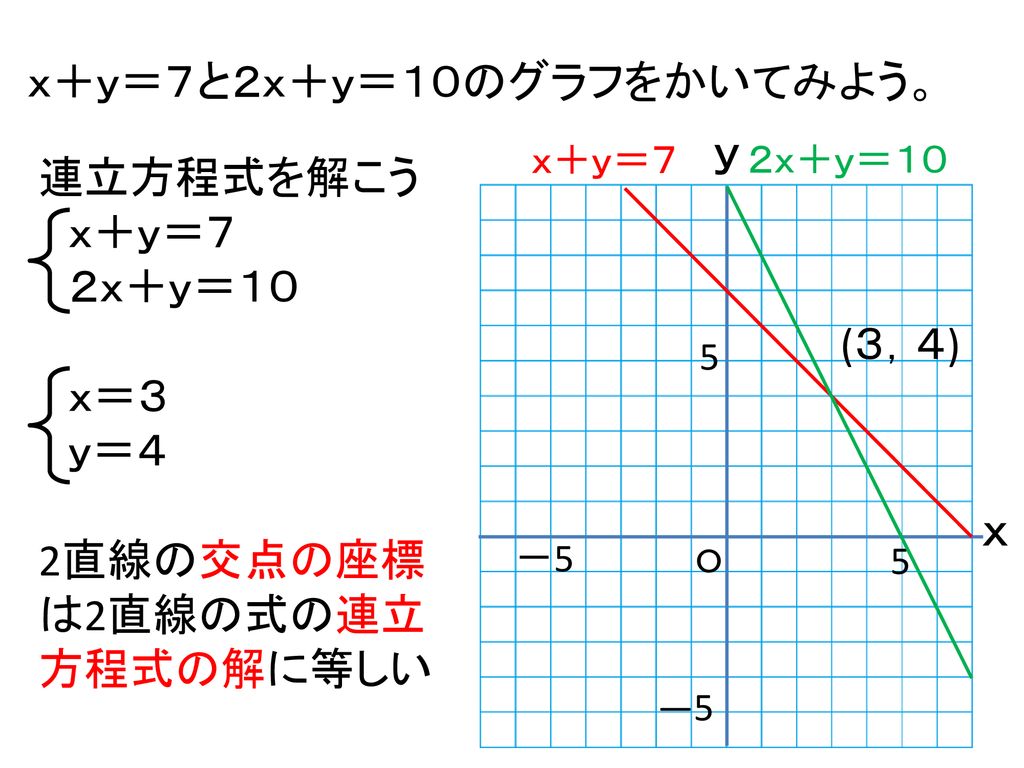
中2 一次関数 連立方程式とグラフ 教科書の問題で、答えが載っていない問題です ⑵の連立方程式の解が見つからない理由の答えを教えてください🙇♀️お願いしますっ💦 グラフにおける連立方程式の意味 連立方程式の解 ⇒連立した方程式の共通解 共通解 ⇒グラフの交点 連立方程式の解 ⇒連立した方程式のグラフの交点 「交点」,「交わる」が問題文章
連立方程式 グラフ 書き方
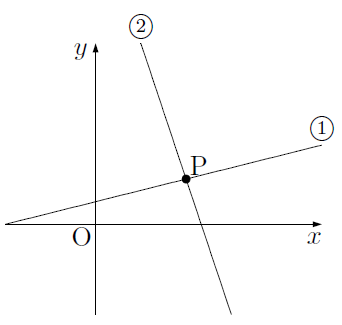
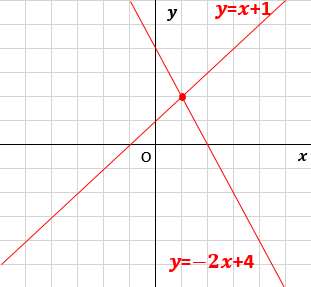
連立方程式 グラフ 書き方-連立方程式 (1) (2)の解は,2つの方程式 (1) (2)を両方とも満たすものですが,これはグラフで考えれば両方の直線上にある点ということになります. したがって,連立方程式の解は2直線の交点の座グラフ作成専用Webアプリ(関数グラフ、方程式の探究、データのプロット、スライダー利用、等々) Graphing Calculator Calculator Suite

中2 連立方程式をグラフで解くやり方 交点の座標を求めてみよう Youtube
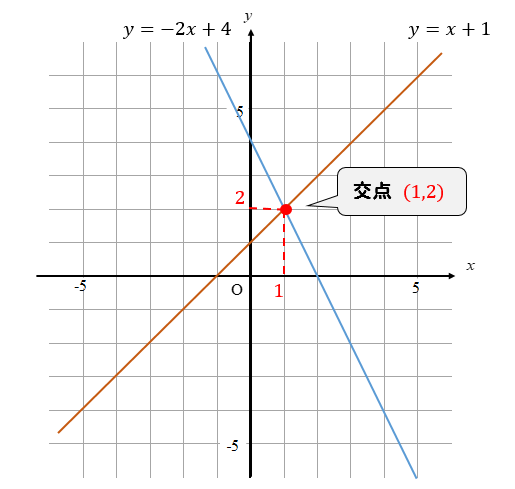
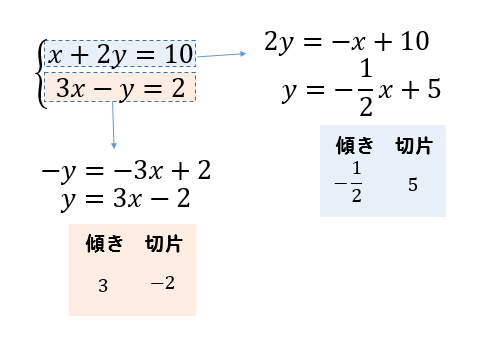
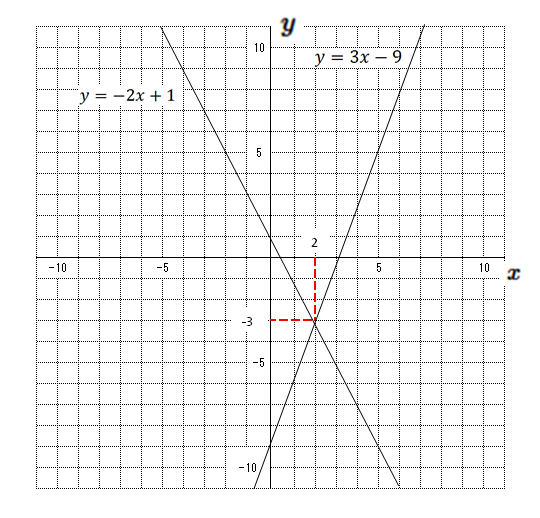
連立方程式をグラフで描く 交点をもとめることで連立方程式を解く実例をみましょう。 方程式のグラフを描くことで連立方程式の解を求めることができます。 次の連立方程式を解いてみましょう連立方程式とグラフ プリント 基礎レベル 基礎1 中2数学一次関数(連立方程式とグラフ) レベル別プリント集 中2数学の一次関数(連立方程式とグラフ)分野について、基礎・応用レベルのプリント教科書の問題で、答えが載っていない問題です⑵の連立方程式の解が見つからない理由の答えを教えてください🙇♀️お願いしますっ💦 問4 x2y=4 3x6y=6 の解が見つからない理由を考えてみよう。
中学数学連立方程式・加減法 中学数学連立方程式・代入法 中学数学連立方程式 小数・分数;電卓の使い方 解を求める連立方程式を①と②を電卓に入力し「計算」ボタンを押してください。 計算方式は加減法・代入法を選択できます。 A=B=Cのような連立方程式を計算する場合は、電卓の① 21年8月19日 / 22年1月29日 前回学習した 「一次関数のグラフ」 中2数学「一次関数のグラフと式」の問題 どこよりも簡単な解き方・求め方 今回は一次関数の「グラフと式
連立方程式 グラフ 書き方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
2 | 2 |  2 |
2 | 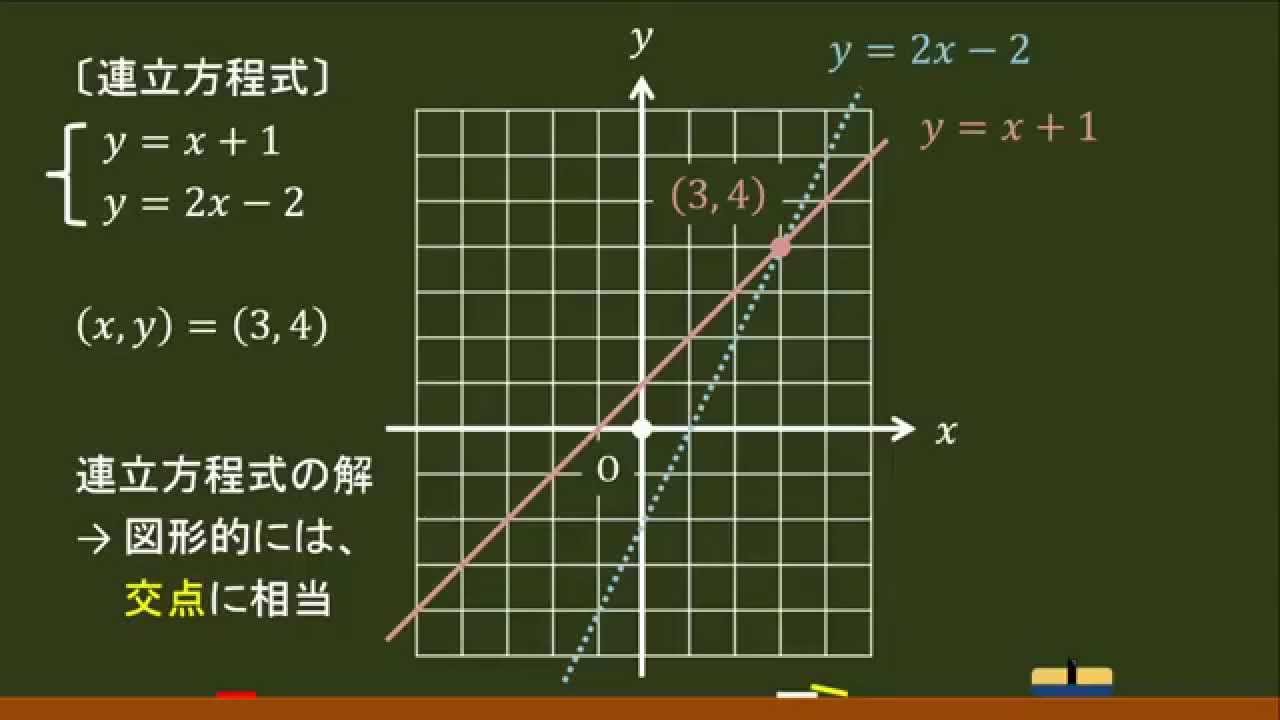 2 | 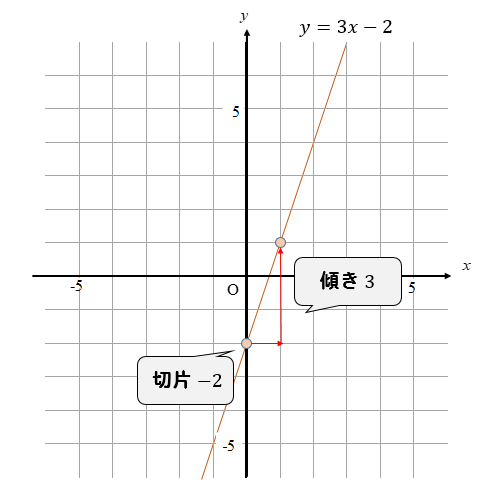 2 |
2 |  2 |  2 |
 2 | 2 | 2 |
 2 |  2 |  2 |
 2 | 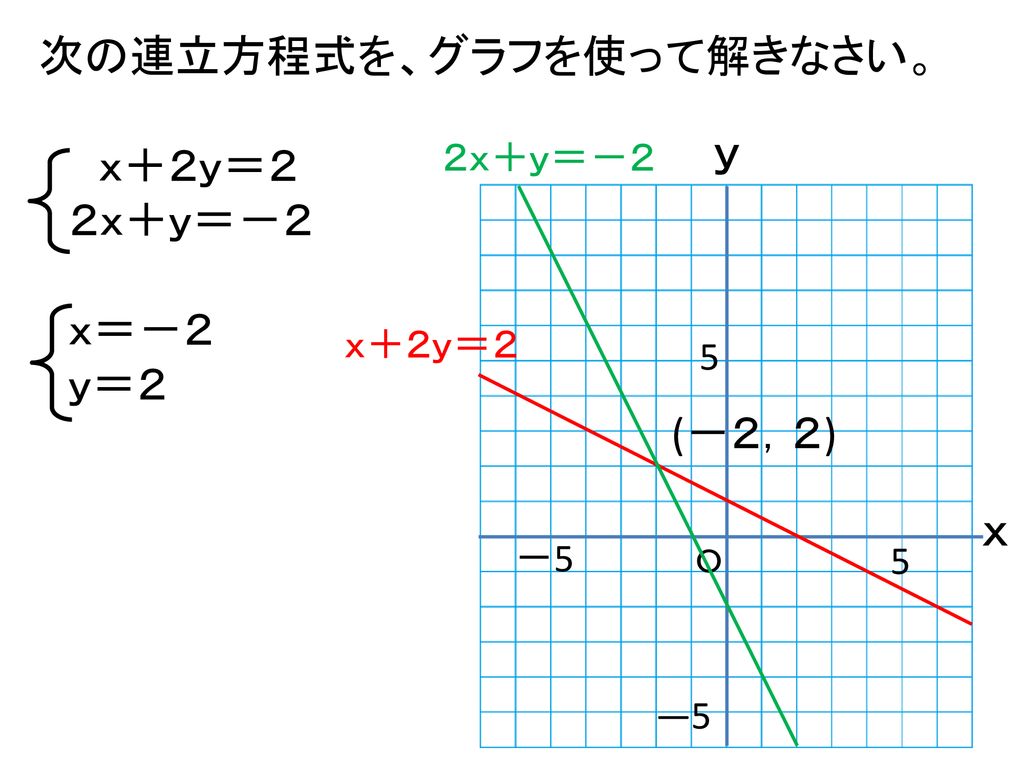 2 | 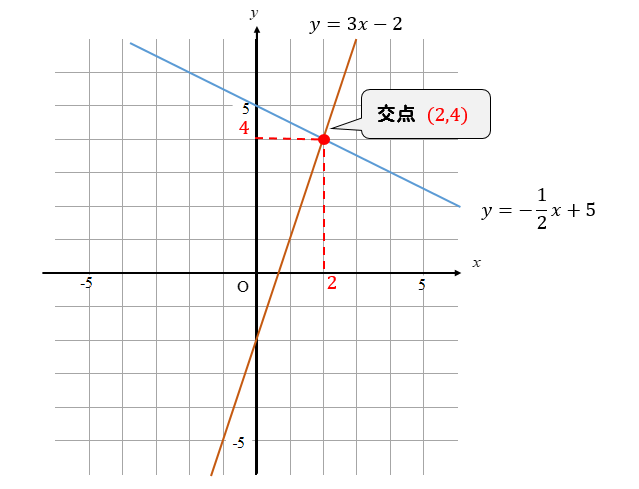 2 |
 2 | 2 | 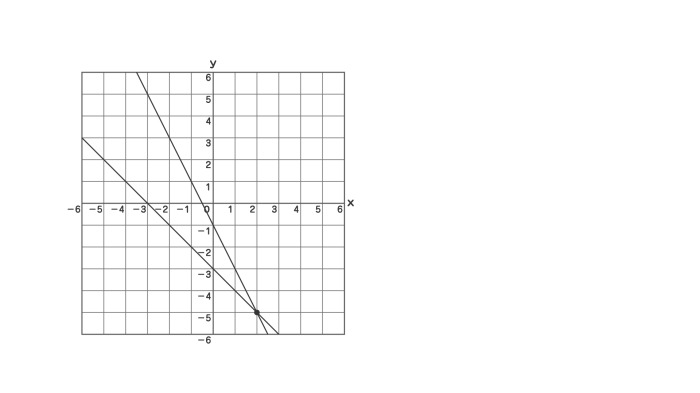 2 |
2 | 2 |  2 |
 2 |  2 | 2 |
2 | 2 | 2 |
 2 |  2 |  2 |
 2 | 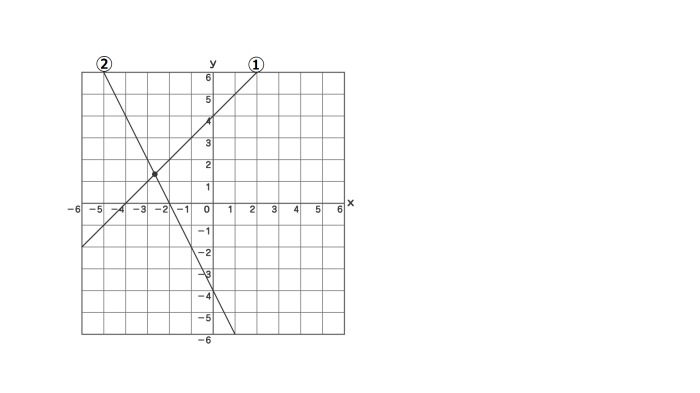 2 | 2 |
 2 |  2 | 2 |
 2 | 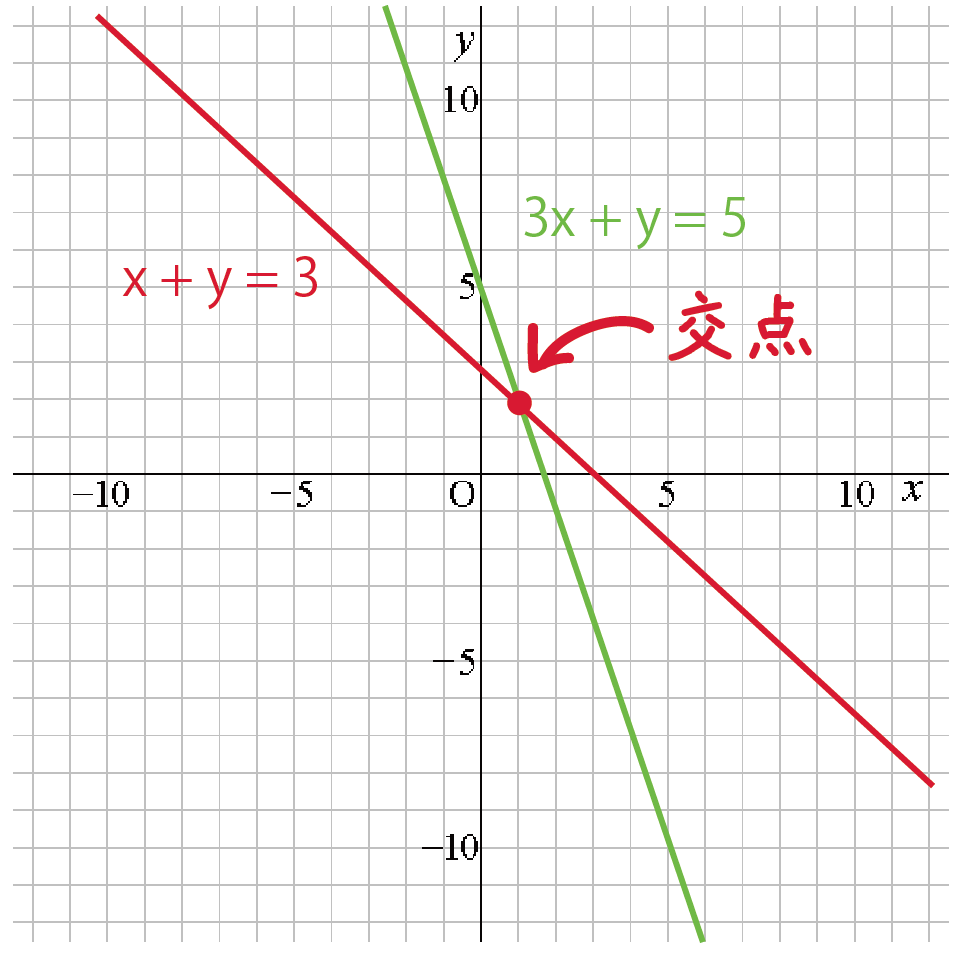 2 | 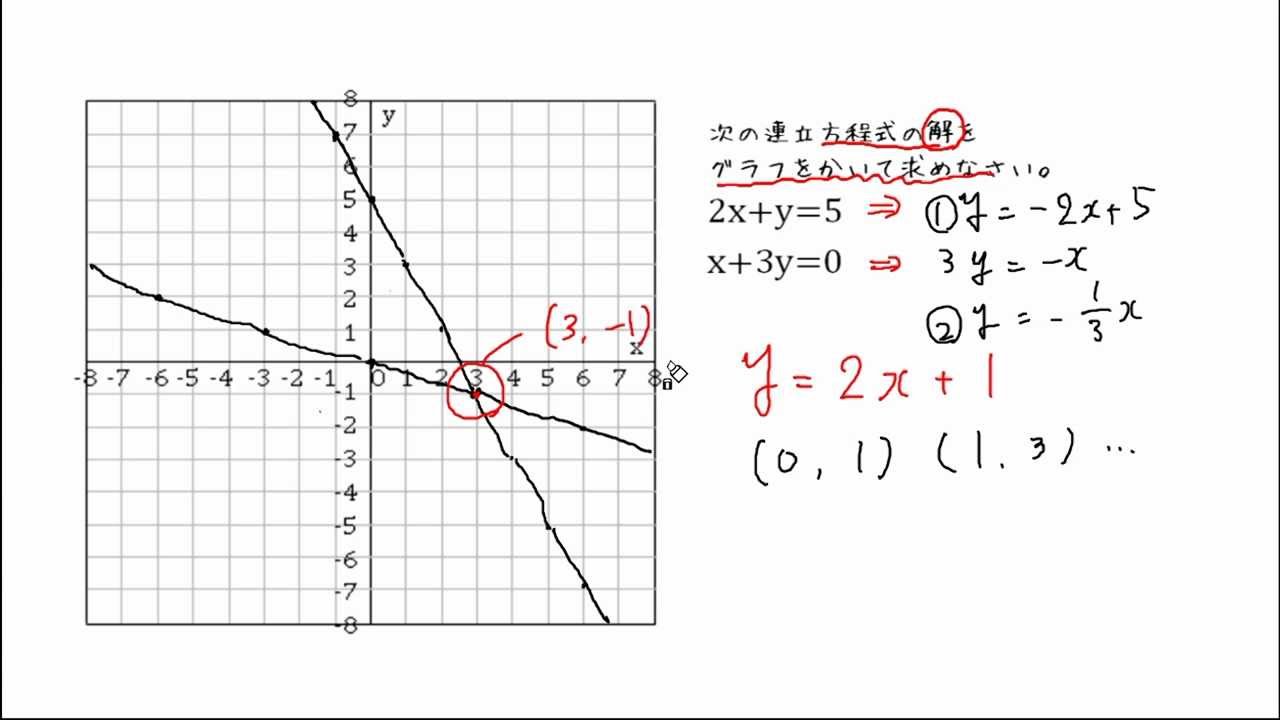 2 |
 2 | 2 |  2 |
 2 | 2 | 2 |
 2 | 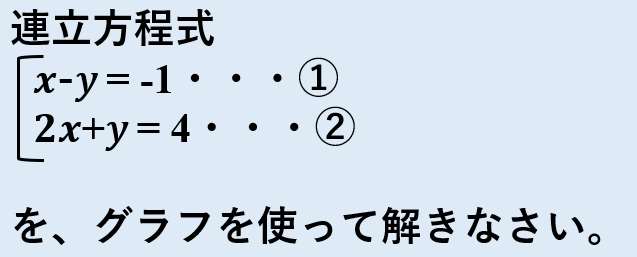 2 | 2 |
2 |  2 | 2 |
 2 |  2 |  2 |
 2 | 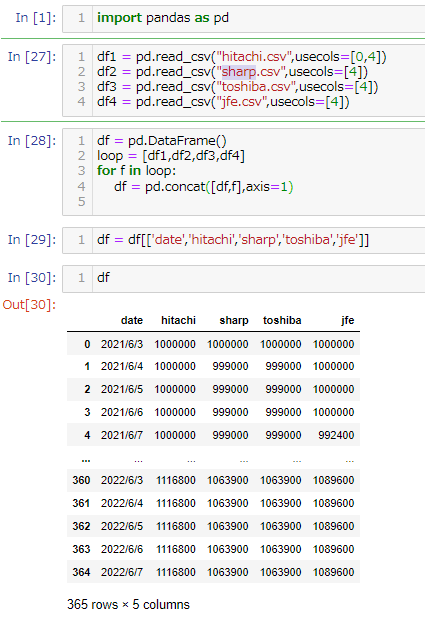 2 |  2 |
 2 |  2 | 2 |
2 | 2 | 2 |
2 | 2 | 2 |
 2 |  2 | 2 |
2 | 2 | 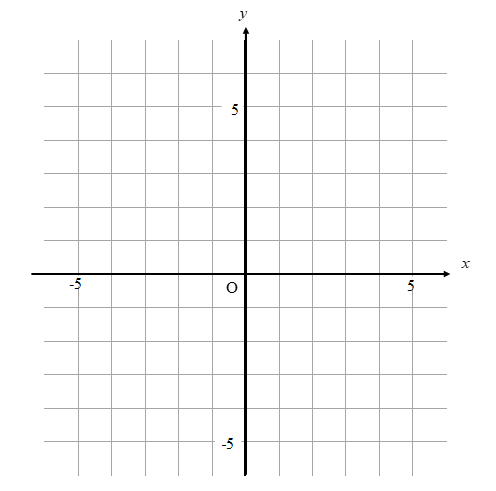 2 |
2 |  2 | 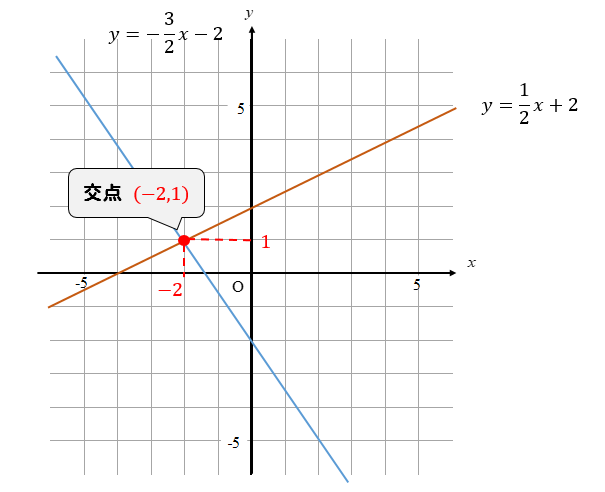 2 |
 2 | 2 | 2 |
 2 |  2 | 2 |
2 |  2 | 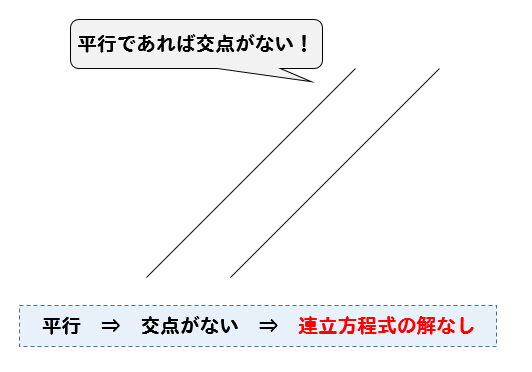 2 |
 2 | 2 | 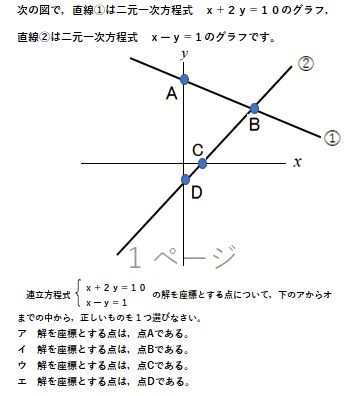 2 |
2 | 2 |  2 |
2 | 2 |  2 |
 2 |  2 |  2 |
 2 |  2 | 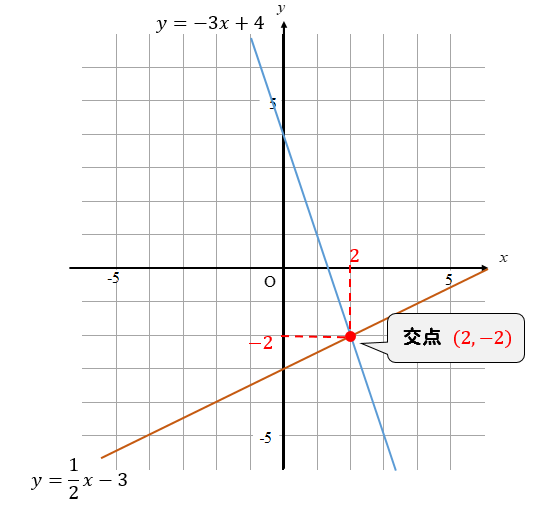 2 |
 2 |  2 |
一次関数 中学数学関数とは何か 中学数学1次関数のグラフ 中学数学1次関数・式 記事の要約 連立方程式のグラフの書き方、解の求め方 グラフが平行になると、解なしになるぞ! スポンサーリンク 目次 連立方程式をグラフを使って解く問題のやり方 手順① 2つ
Incoming Term: 連立方程式 グラフ, 連立方程式 グラフ 書き方, 連立方程式 グラフ 解き方, 連立方程式 グラフ 作成, 連立方程式 グラフ 分数, 連立方程式 グラフ 計算機, 連立方程式 グラフ 問題, 連立方程式 グラフ サイト, 連立方程式 グラフ 平行,




0 件のコメント:
コメントを投稿