√1000以上 一次式とは 数学 245020-一次式とは 数学

2

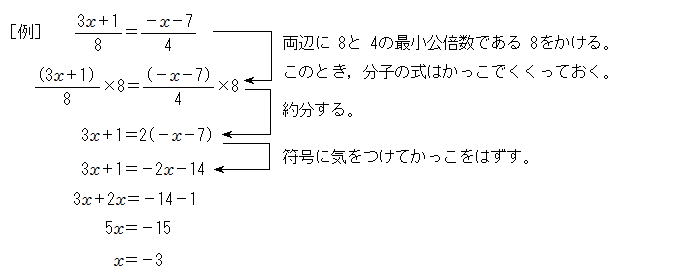
次に、これらの用語をもとに式の計算方法を説明します。 多項式の用語 式 2x－5 を多項式といい、2x と－5 の2つの項からできています。 x の前の数 2 を係数といいます。また、項 2x＝2x 1 の次数は1次で、項 －5＝－5x 0 は0次なので、この多項式は1次式です 左辺は \(3x1\) となり、これは一次式になってしまいます。 よって、この方程式は一次方程式ということになります。 元の方程式に\(x^2\) の項があったとしても、移項してしまえば消えてしまうこともあります。

一次式とは 数学

一次式とは 数学- 一次独立か一次従属かを判定する問題では、最初に「 c 1 a 1 c 2 a 2 ⋯ c n a n = 0 c 1 a 1 c 2 a 2 ⋯ c n a n = 0 」という式を作るのが鉄則です。 なぜこの式を作るかというと、あるベクトルが他のベクトルの一次結合で表せるなら「一次従属」、表せない 一次独立性の使い方（余談） 高校数学の図形問題では一次独立の考え方は以下のような流れで活躍します。 何らかの方法で c 1 v undefined 1 c 2 v undefined 2 = 0 undefined c_1\overrightarrow{v}_1c_2\overrightarrow{v}_2=\overrightarrow{0} c 1 v 1 c 2 v 2 = 0 という式を

中学１年生 数学 方程式の解き方 練習プリント 無料ダウンロード 印刷 このページの答えのプリント 全部

対称式と交代式 対称式 は、 と を入れ替えて にしても、値はもとの式と同じままである。 このように、文字を入れ替えても同じままになる式のことを 対称式（ たいしょうしき）という。, の対称式のうち、式 と 式 の2つを 基本対称式 という。 基本対称式いがいの対称式は、基本対称係数とは？ 係数（けいすう）とは、単項式の数の部分です。文字と数の積で表す式を単項式（たんこうしき）といいます。例えば 3xy の係数は「3」です。上記の単項式は、「3、x、y」の数と文字で表しています。さらに、ある文字に着目して、係数を考える 中1数学にでてくる1次方程式（xの方程式）の解き方 こんにちは！イボコロリを使ってみたKenだよ。 中1数学でむずかしいと言われているのは「方程式」。中1で勉強するのは「 1次方程式 」とよばれているものだ。 なにせ、文字が1つしか含まれていないからね。

合同式(mod)を使うメリット 表記簡略化による本質的な嬉しさ 「 12 12 12 と 7 7 7 を 5 5 5 で割った余りは等しい」と書くよりも 「 12 ≡ 7 (m o d 5) 12\equiv 7\pmod{5} 12 ≡ 7 (mod 5) 」と書く方が楽です。 ほとんど差がないように感じますが，記述式で複雑な問題になると上記のような文言を大量に利益率は1次方程式の、「～を値下げしました」というイメージ図と同じですね。 中学数学で「利益率は?」 という問題はないとは思いますが、 雑学として、「利益率」は、基準が「売値(売上)」 であるということを 知っていて損はないのかなと思います。 利益率はやりたい仕事の指標 全くこの3つの式の関係も「 一次独立 」と言うよ。 最後に重要なことだけど、 未知の定数の数よりも条件式の数の方が多いときは、 それらの式は絶対に一次独立にはならない んだ。 また、 未知の定数の数と同じだけ一次独立な関係の式があれば、

一次式とは 数学のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	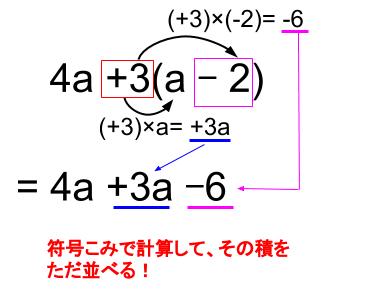第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	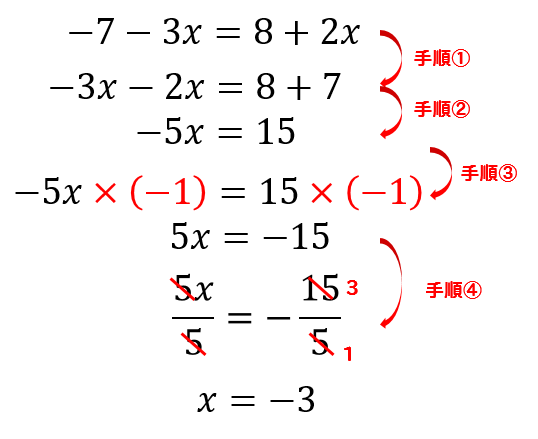第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	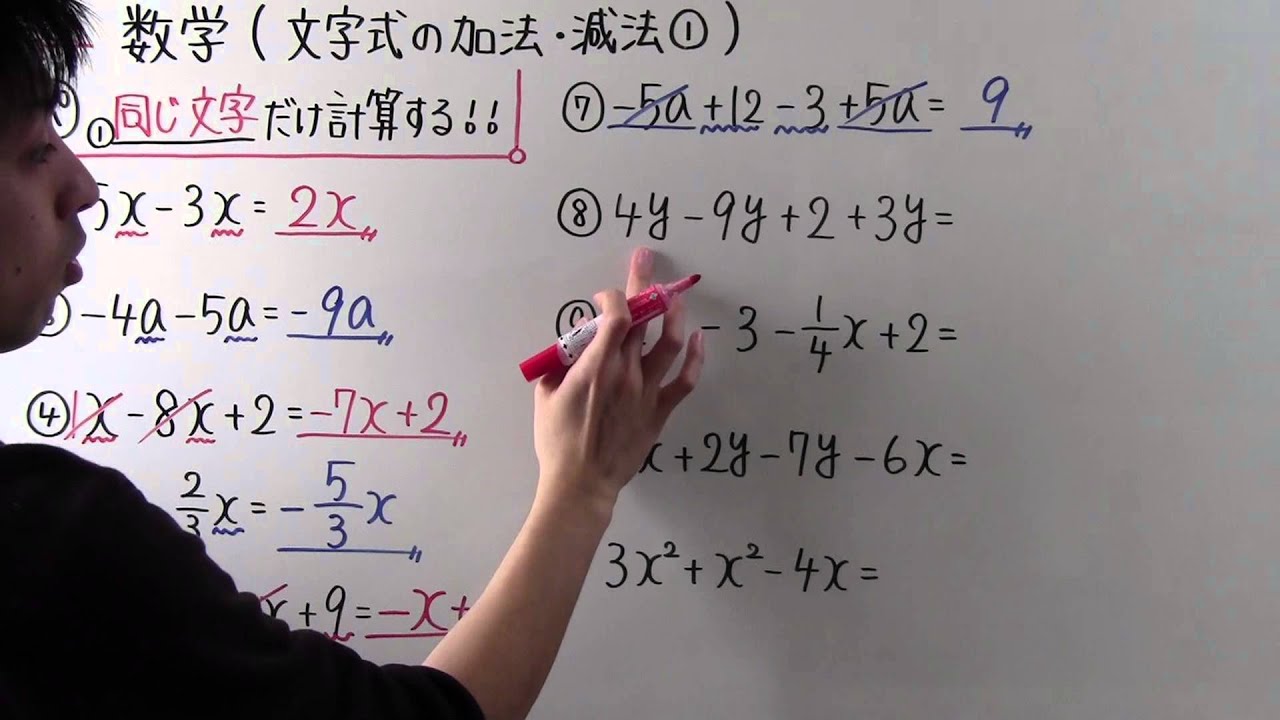第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	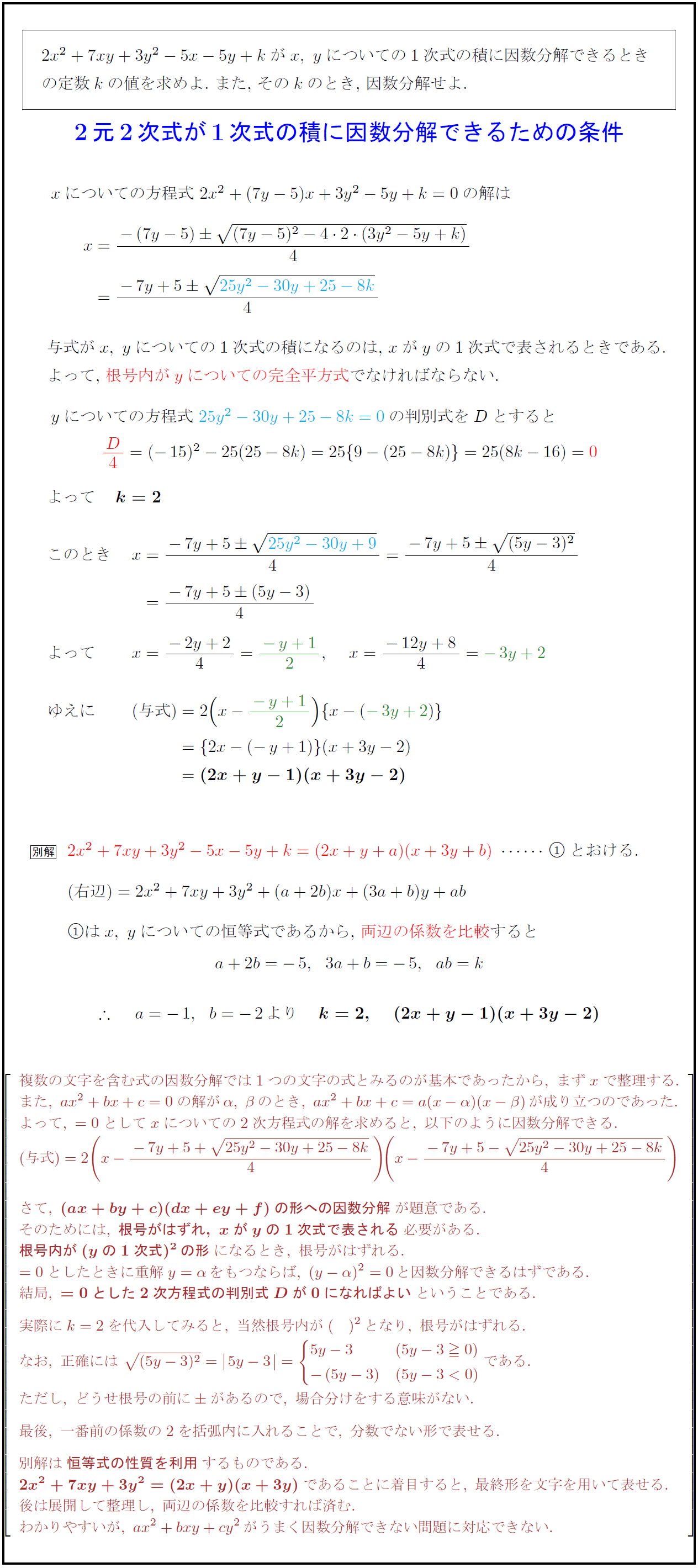第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門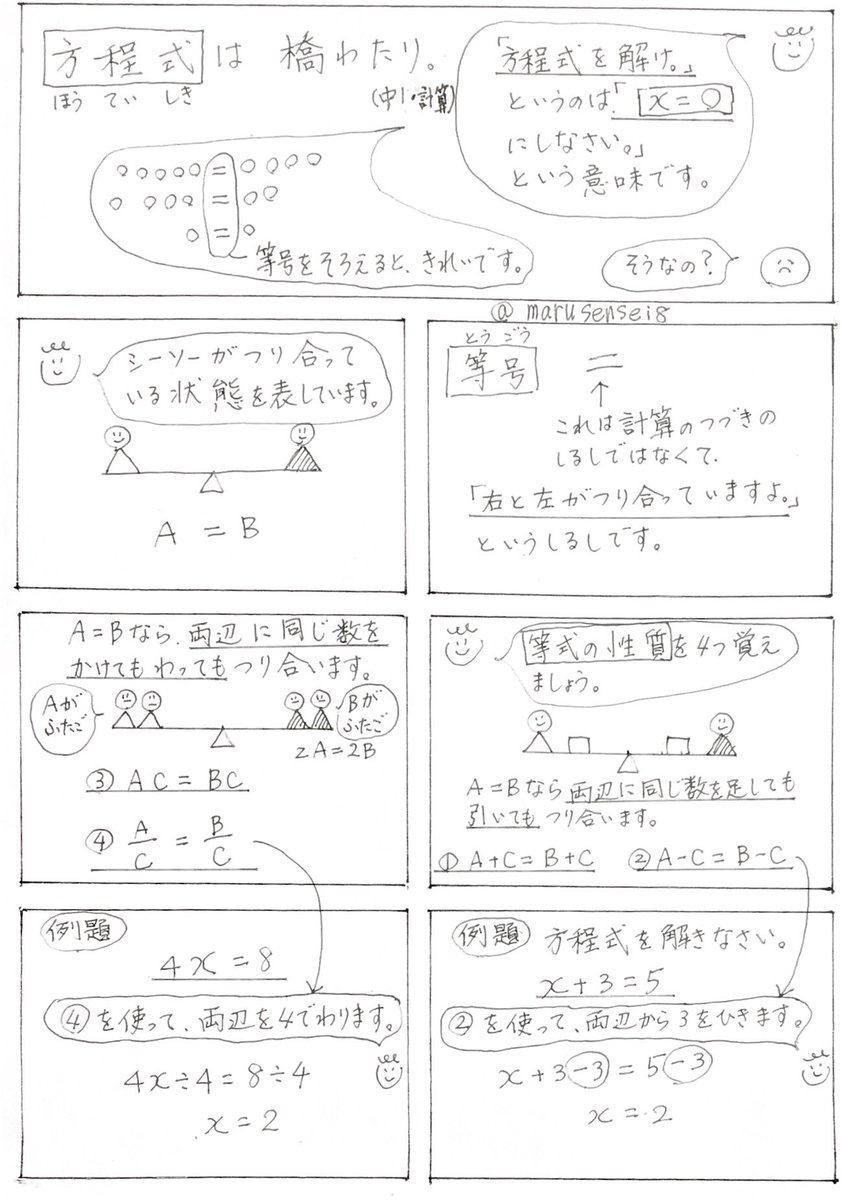
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門
第4回講義 基礎数学 数学入門	第4回講義 基礎数学 数学入門

 文章問題を解いていると、違いがわからなくなってきます。長さ10CMのロウソクは毎分05CMの割合で短くなる。6分後のロウソクの長さは？これは一次関数と一次方程式、二次方程式でも解けますか？ 数学 解決済 教えて！goo9a＋8b は「一次」と「一次」だから「一次式」 6a ＋4b＋7 は「二次」と「一次」と「ゼロ次」だから「二次式」なんだね。 そうですね。項に分けて考えることがポイントですね。 ・分配法則へ進む ・項と係数に戻る ・中学数学計算目次へ戻る ・中学数学

Incoming Term: 一次式とは 数学,